Matemática Sencilla !

Trabajo

T= F .D

El trabajo realizado por una fuerza constante F, aplicada a un cuerpo, que experimenta un desplazamiento d es:

Si el desplazamiento a lo largo de una recta, una distancia X y el Angulo entre la dirección de la fuerza y el desplazamiento es θ.

FUERZA	DISTANCIA	TRABAJO
N	m	n.m=julio
Din	cm	Din.cm=ergio
lb	pie	lb. Pie

1 julio = 10 ergios

POTENCIA

Al definir y calcular trabajo, no hemos desconsiderado el tiempo empleado en su realización, y obviamente, al realizar un trabajo es importante el tiempo invertido; por esta razón definimos la POTENCIA desarrollada como la rapidez con la que se realiza un trabajo:

P=T/t, media en los julios/seg= vatio

Y en el sistema ingles lb pie/seg. También utilizamos un múltiplo del vatio, el kilovatio = 100 vatios y en el sistema ingles el caballo-fuerza (horse-power) HP = 550 lb-pie/seg. El factor-fuerza en vatios es:

1 HP = 746 vatios

Ejemplo: un elevador levanta un carga de 300 N, hasta una altura de 50m en 20seg. ¿Cuál es la potencia desarrollada por el motor que acciona el elevador?

Entonces la fuerza necesaria para levantar la carga es 300 N. La distancia recorrida 50m y el ángulo entre la fuerza (hacia arriba) y el desplazamiento es de 0 grados. Así:

T=F. X=300 N. 50m= 15000 j

P=T/t= 15000 j/20seg= 750 vatios

Cuando un cuerpo sobre el cual se realiza el trabajo se desplaza a velocidad constante, tenemos

P= T/t= = f.v

La potencia se puede calcular como el producto de la fuerza de velocidad.

ENERGIA:

Cuando un cuerpo puede realizar un trabajo decimos que este cuerpo tiene energía. Definimos la energía así:

La energía es la capacidad para realizar un trabajo

La capacidad de realizar un trabajo se genera por diversas causas, por la temperatura que tiene el cuerpo y entonces hablamos de energía térmica; por la configuración atómica y hablamos de energía atómica; y por el movimiento o por la posición.

En la mecánica, nos interesan dos clases de energía:

Energía cinética: EC, es la energía que posee un cuerpo en virtud de su movimiento.

Energía potencial: Ep es la energía que posee un cuerpo en cuerpo de su posición

Cuando un cuerpo realiza o escribe recibe un trabajo, su energía disminuye o aumenta, en una cantidad igual al trabajo o recibido, respectivamente.

Consideramos un cuerpo cuya velocidad inicial es Vo, y sobre el cual actúa una fuerza F a lo largo de una distancia X; si su masa es m, entonces:

a = F/m, juego

V2/f = V2/0 + 2ax

V2/f = V2/0 + 2F/m.x

V2/f = V2/0 + . F x/m, entonces

F . x = ½ m V2/f - ½ m V2/0

En donde la diferencia del segundo miembro corresponde al cambio experimentado en el factor ½ m V2 y el primer miembro es el trabajo realizado por la fuerza F sobre el cuerpo dado.

EC = ½ m V2

Definimos la energía cinética como:

Así, ½ m V2/0 m V2/f corresponde a la energía cinética inicial y final

Respectivamente ejemplo: calcular la energía cinética que posee un móvil de masa 1200 kg que viaja a 72 km/h.

Entonces: m = 1200 kg

V = 72 kg/h = 20m/seg

Luego:

El trabajo realizado para levantar un cuerpo de masa m, una distancia x, por encima de su posición inicial esta dado por:

T = mgx

Si es altura inicial y h su altura final entonces x = h - luego:

T= mg (h- )

T= mgh - mg

Consideramos el trabajo realizado para levantar el mismo cuerpo desde una altura inicial hasta una altura final h, a lo largo de un plano inclinado.

N + F + P= O Y x/s = senθ, s = x/ senθ

(O. n) + (F. o)+ (-p senθ,-p cosθ)

(F-p. senθ, N – p. cosθ) = (0, 0)

F = P senθ;

N = P cosθ.

Luego t = f . s = p senθ. X/senθ = Px

= mgx = mg (h- ) = mgh - mg

De donde concluimos que el trabajo realizado es independiente del camino seguido, y depende solo a las alturas inicial y final. El termino mgh se llama la energía potencial, , del cuerpo.

Esta energía depende de su posición respecto a la tierra y de la tierra gravitacional mg; por ello, usualmente se denomina energía potencial gravitacional.

La suma se denomina energía mecánica total. En ausencia de friccion o cualquier otra fuerza disipadora y si no se agrega energía externa a un sistema, se energía total mecánica permanece constante.

MOVIMIENTO DE TORSION

EQUILIBRIO DE ROTACIÓN

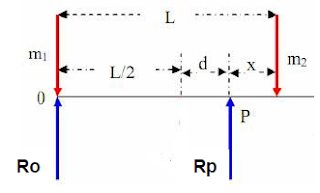
1. Una viga uniforme de longitud L sostiene bloques con masas m1 y m2 en dos

posiciones, como se ve en la figura. La viga se sustenta sobre dos apoyos puntuales. ¿Para qué valor de X (en metros) estará balanceada la viga en P tal que la fuerza de reacción en O es cero?.

Datos:

L = 7 m

d = 1 m

m1 = 2,5 kg

m2 = 9 kg

1. Escriba las condiciones necesarias para equilibrio del cuerpo que se muestra en la figura p12.2. Tome el origen de la Ecuación del par de torsión en el punto o.

3.Una escalera uniforme de longitud L y masa m₁se apoya contra una pared sin fricción. La escalera forma un ángulo θ con la horizontal. (a) Encuentre las fuerzas horizontal y vertical que el suelo ejerce sobre la base de la escalera cuando un bombero de masa m₂está a una distancia x de la base. (b) Si la escalera está a punto de resbalar cuando el bombero está a una distancia d de la base, ¿cuál es el coeficiente de fricción estática entre la escalera y el suelo.